基本情報技術者試験 令和7年度 科目A 公開問題(過去問) 問3 について解説します。
問題
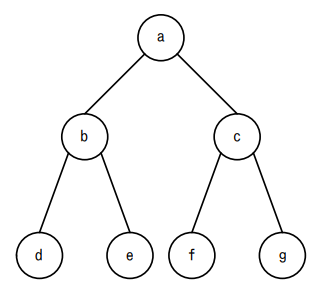
問3 図の木構造は2分探索木である。a~gの値の大小関係として、適切なものはどれか。ここで、a~gの値は重複しないものとする。
ア a < b < d < e < c < f < g
イ d < b < e < a < f < c < g
ウ d < e < f < g < b < c < a
エ g < f < c < e < d < b < a
解説・解答
2分探索木の基本ルール
2分探索木では、各ノードXについて次が成り立ちます。
・左部分木にある値はすべてXより小さい
・右部分木にある値はすべてXより大きい
ルールを上から順に当てはめて不等号を作成
※a~gは重複なしなので「<」か「>」で必ず決まります。
(1) 根 a に注目
左部分木(b, d, e)は aより小さい
b < a
d < a
e < a
右部分木(c, f, g)は aより大きい
a < c
a < f
a < g
つまり、(d, b, e) < a < (f, c, g) が確定します。
(2) b(aの左側の部分木)に注目
b について2分探索木のルールを適用すると、
bの左部分木は bより小さい → d < b
bの右部分木は bより大きい → b < e
よって、d < b < e が確定。
さらに、この部分木全体が a より小さいので、d < b < e < a となります。
(3) c(aの右側の部分木)に注目
c について2分探索木のルールを適用すると、
cの左部分木は cより小さい → f < c
cの右部分木は cより大きい → c < g
よって、f < c < g が確定。
さらに、この部分木全体が a より大きいので、a < f < c < g となります。
上記(1)~(3)をつなげると、d < b < e < a < f < c < g となります。
以上により、この問題の解答は「イ」になります。

