基本情報技術者試験 令和6年度 科目B 公開問題(過去問) 問3 について解説します。
問題
問3 次のプログラム中の〔 〕に入れる正しい答えを、解答群の中から選べ。ここで、配列の要素番号は 1 から始まる。
図1に示すグラフの頂点には、1から順に整数で番号が付けられている。グラフは無向グラフであり、各頂点間には高々一つの辺がある。一つの辺は両端の頂点の番号を要素にもつ要素数2の整数型の配列で表現できる。例えば、{1, 3} は頂点1と頂点3を端点とする辺を表す。グラフ全体は、グラフに含まれる辺を表す要素数2の配列を全て格納した配列(以下、「辺の配列」という)で表現できる。辺の配列の要素数はグラフの辺の個数と等しい。図1のグラフは整数型配列の配列{{1, 3}, {1, 4}, {3, 4}, {2, 4}, {4, 5}}と表現できる。
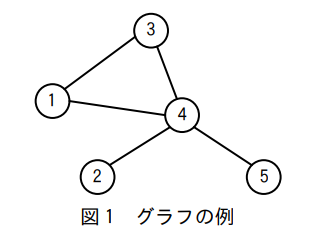
関数 edgesToMatrix は、辺の配列を隣接行列に変換する。隣接行列とは、グラフに含まれる頂点の個数と等しい行数および列数の正方行列で、 i 行 j 列の成分は頂点 i と頂点 j を結ぶ辺があるときに 1 となり、それ以外は 0 となる。行列の対角成分は全て 0 で、無向グラフの場合は対称行列になる。図1のグラフを表現する隣接行列を図2に示す。
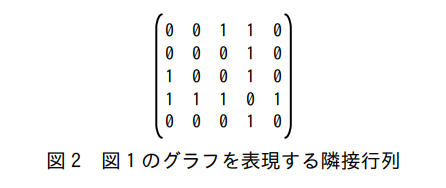
関数 edgesToMatrix は、引数 edgeList で辺の配列を、引数 nodeNum でグラフの頂点の個数をそれぞれ受け取り、隣接行列を表す整数型の二次元配列を返す。
[プログラム]
○整数型の二次元配列: edgesToMatrix(整数型配列の配列: edgeList,
整数型: nodeNum)
整数型の二次元配列: adjMatrix ← {nodeNum行nodeNum列の 0}
整数型: i, u, v
for (i = 1 から edgeList の要素数 まで 1 ずつ増やす)
u ← edgeList[i][1]
v ← edgeList[i][2]
〔 〕
endfor
return adjMatrix
解答群
ア adjMatrix[u, u] ← 1
イ adjMatrix[u, u] ← 1
adjMatrix[v, v] ← 1
ウ adjMatrix[u, v] ← 1
エ adjMatrix[u, v] ← 1
adjMatrix[v, u] ← 1
オ adjMatrix[v, u] ← 1
カ adjMatrix[v, v] ← 1
解説・解答
関数 edgesToMatrix の入力は、辺の配列 edgeList とグラフの頂点の個数 nodeNum です。
例のグラフは、次のような「線の一覧」で表されています。
・{1, 3}
・{1, 4}
・{3, 4}
・{2, 4}
・{4, 5}
この配列が edgeList で、1つ1つが「頂点 u と頂点 v を結ぶ線」です。
この場合のグラフの頂点の個数 nodeNum は 5 です。
関数 edgesToMatrix の出力は、隣接行列 adjMatrix です。隣接行列は、次のような表です。
| 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|
| 1 | 0 | 0 | 1 | 1 | 0 |
| 2 | 0 | 0 | 0 | 1 | 0 |
| 3 | 1 | 0 | 0 | 1 | 0 |
| 4 | 1 | 1 | 1 | 0 | 1 |
| 5 | 0 | 0 | 0 | 1 | 0 |
行の番号は出発する頂点、列の番号は到着する頂点です。
線があればマスの中身は「1」、線がなければマスの中身は「0」です。
例えば、「1 行 3 列」が 1 なので「頂点1と頂点3はつながっている」と分かります。
プログラムの流れは次のようになります。
1. 最初に表を全てのマスを 0 にして作る。(この時点では、どの頂点もまだ線がない状態。)
2. for文のループで、edgeList に入っている線を1本ずつ取り出す。
edgeList[i] … i 本目の線
edgeList[i][1] … その線の片方の頂点 → u に格納
edgeList[i][2] … その線のもう片方の頂点 → v に格納
つまり、ループ1回で「頂点 u と頂点 v の間に線がある」という情報を手に入れている。
3. 「頂点 u と頂点 v の間に線がある」ということを隣接行列 adjMatrix に書き込む。
※この書き込む部分が〔 〕で、本問題で問われている部分です。
問題文にはグラフは無向グラフと書かれています。無向グラフは「1 → 3」も「3 → 1」も区別せず、「1 と 3 がつながっているだけ」と考えるグラフです。
「1 と 3 がつながっている」なら隣接行列の
・1 行 3 列 も 1
・3 行 1 列 も 1
というように必ず対称になります。
つまり、線 {u, v} があったら、adjMatrix[u, v] を 1 にすると同時に、adjMatrix[v, u] も 1 にする必要があります。この部分の処理はプログラムでは次のように記述します。
adjMatrix[u, v] ← 1
adjMatrix[v, u] ← 1
以上により、この問題の解答は「エ」になります。

