基本情報技術者試験 令和6年度 科目B 公開問題(過去問) 問5 について解説します。
問題
問5 次のプログラム中の〔 a 〕~〔 c 〕に入れる正しい答えの組合せを、解答群の中から選べ。ここで、配列の要素番号は 1 から始まる。
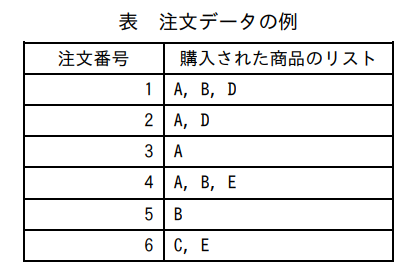
一度の注文で購入された商品のリストを、注文ごとに記録した注文データがある。表に、注文データの例を示す。
注文データから、商品 x と商品 y とが同一の注文で購入されやすい傾向を示す関連度 L_xy を、次の式で計算する。
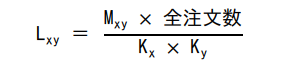
ここで、M_xy は商品 x と商品 y とが同一の注文で購入された注文数、K_x は商品 x が購入された注文数、K_y は商品 y が購入された注文数を表す。表の例では、M_AB が 2、全注文数が 6、K_A が 4、K_B が 3 であるので、商品 A と商品 B の関連度 L_AB は、(2 × 6) / (4 × 3) = 1.0 である。
手続 putRelatedItem は、大域変数 orders に格納された注文データを基に、引数で与えられた商品との関連度が最も大きい商品のうちの一つと、その関連度を出力する。プログラムでは、商品は文字列で表し、注文は購入された商品の配列、注文データは注文の配列で表している。注文データには2種類以上の品目が含まれるものとする。また、注文データにある商品以外の商品が、引数として与えられることはないものとする。
[プログラム]
// 注文データ(ここでは表の例を与えている)
大域:文字列型配列の配列:orders ← { {“A”, “B”, “D”}, {“A”, “D”}, {“A”},
{“A”, “B”, “E”}, {“B”}, {“C”, “E”} }
○putRelatedItem(文字列型:item)
文字列型の配列:allItems ← ordersに含まれる文字列を
重複なく辞書順に格納した配列
// 表の例では {“A”, “B”, “C”, “D”, “E”}
文字列型の配列:otherItems ← allItems の複製から値が item である
要素を除いた配列
整数型:i, itemCount ← 0
整数型の配列:arrayK ← {otherItems の要素数個の 0}
整数型の配列:arrayM ← {otherItems の要素数個の 0}
実数型:valueL, maxL ← -∞
文字列型:order
文字列型:relatedItem
for (order ← orders の要素を順に代入する)
if (order のいずれかの要素の値が item の値と等しい)
itemCount の値を 1 増やす
endif
for (i を 1 から otherItems の要素数まで 1 ずつ増やす)
if (order のいずれかの要素の値が otherItems[i] の値と等しい)
if (order のいずれかの要素の値が item の値と等しい)
〔 a 〕の値を 1 増やす
endif
〔 b 〕の値を 1 増やす
endif
endfor
endfor
for (i を 1 から otherItems の要素数まで 1 ずつ増やす)
valueL ← (arrayM[i] ×〔 c 〕) ÷ (itemCount × arrayK[i])
/* 実数として計算する */
if (valueL が maxL より大きい)
maxL ← valueL
relatedItem ← otherItems[i]
endif
endfor
relatedItem の値と maxL の値をこの順にコンマ区切りで出力する
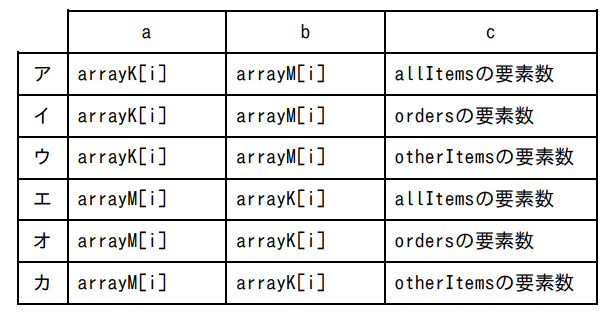
解答群
解説・解答
プログラムが行いたいこと
関連度 L_xy は次の式で定義されています。
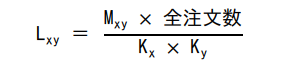
M_xy: 商品xと商品yを両方含む注文数
K_x: 商品xを含む注文数
K_y: 商品yを含む注文数
全注文数: すべての注文の件数
手続 putRelatedItem(item) は、商品x(=引数 item)と最も関連度が高い別の商品yと、そのときの関連度 L_xy を求めて出力します。
データ構造の確認
(1) 注文データ orders
orders = {
{ “A”, “B”, “D” },
{ “A”, “D” },
{ “A” },
{ “A”, “B”, “E” },
{ “B” },
{ “C”, “E” }
}
1つ目の要素は {A, B, D} という注文、2つ目の要素は {A, D} という注文、…という形で1件分の注文が文字列の配列になります。orders の要素数 = 全注文数 となります。(ここでは 6 になります。)
(2) allItems と otherItems
allItems ← ordersに含まれる文字列を重複なく辞書順に格納した配列
otherItems ← allItemsの複製から値がitemである要素を除いた配列
表の例では allItems = { “A”, “B”, “C”, “D”, “E” } ですので、例えば item = “A” のときは otherItems = { “B”, “C”, “D”, “E” } となります。つまり、商品xが item、商品yが otherItems[i](i番目の別の商品)という対応になります。
プログラムの確認
【最初の for 文 の部分】
itemCount ← 0
…
for (order ← orders の要素を順に代入する)
if (order のいずれかの要素の値が item の値と等しい)
itemCount の値を 1 増やす
endif
…
endfor
注文データ orders から各注文を1件ずつ取り出して order に代入し、その注文に item が含まれていれば itemCount の値を1増やしますので、itemCount は商品xを含む注文の数で itemCount = K_x になります。
(例)item = “A” の場合
Aを含む注文は注文番号1, 2, 3, 4の4件なので itemCount = 4 となり、K_A は4です。
【次の二重ループの for 文 の部分】
for (order ← orders の要素を順に代入する)
…
for (i を 1 から otherItems の要素数まで 1 ずつ増やす)
if (order のいずれかの要素の値が otherItems[i] の値と等しい)
if (order のいずれかの要素の値が item の値と等しい)
〔 a 〕の値を 1 増やす
endif
〔 b 〕の値を 1 増やす
endif
endfor
endfor
外側のfor文は全ての注文を順番に見ていくというものです。内側のfor文はotherItems[i]をi = 1,2,… と変えながら商品yを見ていくというものです。
「if (order の… が otherItems[i] の値と等しい)」ではこの注文に商品yが含まれているかを判定し、商品yが含まれていれば、次に「if (order の… が item の値と等しい)」でこの注文に商品xも含まれているかを判定しています。商品xも含まれていれば〔 a 〕の値を 1 増やしています。商品xが含まれていなくても商品yが含まれているので、商品xが含まれていてもいなくても〔 b 〕の値を 1 増やしています。これより、〔 a 〕と〔 b 〕は次のようになります。
〔 a 〕:「商品xと商品yを両方含む注文数 M_xy」の配列 → arrayM[i]
〔 b 〕:「商品yを含む注文数 K_y」の配列 → arrayK[i]
【最後の for 文 の部分】
for (i を 1 から otherItems の要素数まで 1 ずつ増やす)
valueL ← (arrayM[i] ×〔 c 〕) ÷ (itemCount × arrayK[i])
/* 実数として計算する */
…
endfor
「valueL ← (arrayM[i] ×〔 c 〕) ÷ (itemCount × arrayK[i])」について、ここまでで分かった arrayM[i] = M_xy、itemCount = K_x、arrayK[i] = K_y を代入すると下記のようになります。
valueL = (M_xy ×〔 c 〕) ÷ (K_x × K_y)
この式を問題文の定義式
L_xy = (M_xy × 全注文数) ÷ (K_x × K_y)
と全く同じ形にするには〔 c 〕は「全注文数」でなくてはなりません。
「全注文数」とは注文データの件数で、注文データは配列 orders に格納されているため、
全注文数 = orders の要素数
となり、〔 c 〕は「orders の要素数」が入ります。
したがって、〔 a 〕は arrayM[i]、〔 b 〕は arrayK[i]、〔 c 〕は orders の要素数 が入ります。
以上により、この問題の解答は「オ」になります。

